,,Lesekurs: Surgery theory``


Ein wichtiges Ziel der Topologie ist es, kompakte Mannigfaltigkeiten ohne Rand zu klassifizieren. Dazu wurde eine ausgefeilte Theorie entwickelt (``Schneiden und Kleben'' oder ``Chirurgie'' bzw. englisch ``Surgery''). Diese verbindet Bündeltheorie, Algebra (insbesondere quadratischer Formen) und geometrische Analysis zu einem sehr erfolgreichen ganzen; führt dabei zu tiefliegenden offenen Fragestellungen und Vermutungen aus der aktuellen Forschung (Novikov-Vermutung, Borel-Vermutung, Farrell-Jones- und Baum-Connes -Isomorphismus Vermutung).

Wir wollen die Grundlagen dieser Theorie und einige ihrer Anwendungen kennenlernen. Quellen für den Lesekurs sind dabei relativ aktuell entstandene Lehrbücher, ich denke momentan insbesondere an diejenigen von Ranicki und Lück. Genaueres wird noch festgelegt.

Ein Ziel des Lesekurs ist es, die Surgery-Vorträge des Seminars Mapping Surgery to Analysis vorzubereiten.

Zur Vorgehensweise: wir werden Kapitelweise unsere Quelle lesen (wobei vorher ein Überblick über die wichtigsten Punkte gegeben werden soll), und dann während der Treffen zusammen Fragen zum Stoff diskutieren.

Literatur

(KL) Kreck and Lück; The Novikov conjecture: Geometry and Algebra, Birkhäuser
(L) Lück; A basic introduction to surgery theory
(R) Ranicki; Algebraic and geometric surgery, Cambridge University Press
(W) Wall; Surgery on compact manifolds

Im Lesekurs werden wir das Buch von Ranicki benutzen, darauf beziehen sich auch alle Angaben im Zeitplan.

Zeitplan

Thema Termin Aufgaben
Kap 1,2 Fr, 9.3.06, 10:00, Emmy-Noether Raum verstehe 2.7-2.10, 2.24, 2.25
Kap 3,4, 5.1,5.2 Do, 23.3., 14:15, Emmy-Noether Raum A2
Kap 5 Do, 30.3., 14:15, Emmy-Noether Raum A3

A2: konzentrieren auf 3.4, 3.13-3.15, 3.20,3.21 (weniger die Steenrod squares), 3.25,3.26
3.20 mit Beweis, 3.33
4.1,4.4,4.7 (Orientierungscharakter ggf. ignorieren), 4.10 wichitg für ``surgery to analysis'', aber nicht für die Chirurgietheorie
4.16-4.22 im Detail. Section 4.3 kann weggelassen werden. 4.37, 4.43, 4.55, 4,58 mit Beweis.
4.62 ausarbeiten, 4.65, 4,68

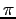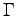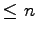A3, Important Points: Exercise 5.2: Prove that bundles over $ S^n$ with fiber $ F$ are in one-to-one correspondence to homotopy classes of maps $ S^{n-1}\to Homeo(F)$.
5.3, statement of 5.6, 5.8, 5.9 5.15; work out 5.19, statement of 5.23, 5.29, 5.30 --work out why 5.30 (ii) is not a good definition (keyword: automorphisms!), 5.35, 5.39, 5.42, 5.49 (provided, the tangent bundle is known, else look at 5.47), 5.50,5.5-5.62, 5.63-5.64 in detail. Work out 5.69
leave out 5.5: not relevant for the development of surgery theory


Teilnehmer