Proseminar ``Analysis der Zahlen''
- Interessentenkreis: Studierende nach dem 1. Semester
- Dozenten: Thomas Schick und NN.
- Thema:
Analysis der Zahlen
- Vorbesprechung: Do, 25.1., 13:00-14:00 im Sitzungssaal
Zahlen (insbesondere reelle und komplexe) sind das ``Handwerkszeug'' der
Analysis; au"serdem nat"urlich auch fundamental f"ur viele andere Bereiche der
Mathematik und dar"uber hinaus. Viele interessante und verbl"Uffende
Eigenschaften von Zahlen lassen sich mit analytischen Methoden nachweisen, die
alleine auf dem Stoff des 1. Semesters aufbauen (diese Theorie f"uhrt
nat"urlich weiter, bis zu heute aktueller Forschung und ber"uhmten ungel"osten
Problemen wie der Riemannschen Vermutung).
Wir werden uns einige spezielle Aspekte anschauen (die in sich immer wieder
abgeschlossen sind), insbesondere zu folgenden Fragestellungen (die teilweise
etwas "uber ``Analysis von Zahlen'' hinausgehen); genauere Details werden bis
zur Vorbesprechung ausgearbeitet.
- Zur Zahl
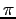 (Geschichte, N"aherungswerte, Charakterisierungen,
Formeln) [[Ee, Kapitel 5, insbes 5.1.3, 5.4.1,5.4.4, 5.4.3] [MT History of
(Geschichte, N"aherungswerte, Charakterisierungen,
Formeln) [[Ee, Kapitel 5, insbes 5.1.3, 5.4.1,5.4.4, 5.4.3] [MT History of 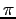 ]
]
- mehr zur Zahl
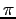 , insbesondere Irrationalit"at von
, insbesondere Irrationalit"at von 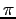 . [Ee, Kap 5], [K], [Ko], [Ee 5.4.6] [St 6.2,6.3]
. [Ee, Kap 5], [K], [Ko], [Ee 5.4.6] [St 6.2,6.3]
- Transzendente Zahlen und Transzendenz von e [JMP 7.2], [Ko 4, A12], [Sp S. 362],
[Si], [K]
- Nullstellen komplexer Polynome, Fundamentalsatz der Algebra [E 4.3, 4.2]
- Transzendenz von
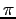 I[JMP 7.3-7.6], [L], [H]
I[JMP 7.3-7.6], [L], [H]
- Transzendenz von
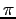 II [JMP 7.3-7.6], [L], [H]
II [JMP 7.3-7.6], [L], [H]
- Die Stirlingsche Formel f"ur n! [Ko 8., 8.6]
- Die
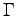 -Funktion und einige ihrer Eigenschaften [Ko 18]
-Funktion und einige ihrer Eigenschaften [Ko 18]
- Primzahlen, insbesondere ihre Anzahl
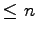 [Z]
[Z]
- Der Primzahlsatz [S] (nicht leicht, vielleicht 2 Vortr"age)
- Kettenbr"uche I+II [R 12.2, 12.3, 12.4], [Ch 1-6,9]
- Approximationseigenschaften der Fourier-Polynome und Fourierreihen? [Ko]
- Weierstra"s Satz "uber Polynomapproximationen? [Ko S.341]
- Nullstellen von Polynomen vom Grad 3 und 4 (?)
Literatur
- A
- Apostol: Introduction to analytic number theory; Springer
- Ch
- Chintchine: Kettenbr"uche, Teubner Leipzig
- Ee
- Ebbinghaus e.a.: Zahlen (2. Auflage); Springer 1988
- H
- Hilbert: Gesammelte Werke I
- JMP
- Jones, Morris, Pearson: Famous Impossibilities
- K
- Karcher: Monotoniesatz und Transzendenz von e. Math. Semesterber. 33 (1986), no. 1, 84-116.
- Ko
- Königsberger: Analysis I
- L
- Lindemann: "Uber die Zahl
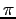 , Math. Ann. 20, 213-225.
, Math. Ann. 20, 213-225.
- MT
- The MacTutor history of math archive
- R
- Rosen: Elementary number theory and its applications 5th
ed. Addison-Wesley 2004
- S
- Selberg: An elementary proof of the prime number theorem, Annels of
Mathematics 50 (1949), 305-313,
http://han.sub.uni-goettingen.de/han/5310/www.jstor.org/cgi-bin/jstor/printpage/0003486x/di961711/96p0056t/0?frame=noframe&dpi=3&userID=864ca38c@uni-goettingen.de/01cc99332600501b50b59&backcontext=table-of-contents&backurl=/cgi-bin/jstor/listjournal/0003486x/di961711
- Si
- Transzendente Zahlen. B. I. Hochschultaschenbücher, Band 137*. Bibliographisches Institut, Mannheim 1967 86 pp.
- Sp
- Calculus on manifolds. A modern approach to classical theorems of advanced calculus. W. A. Benjamin, Inc., New York-Amsterdam 1965 xii+144 pp.
- St
- Steward: Galois Theory, Chapman and Hall 2004
- Z
- Zagier: Die ersten 500 Millionen Primzahlen. Living numbers,
pp. 39-73, Math. Miniaturen, 1, Birkhäuser, Basel-Boston, Mass., 1981, oder
Mathematical Intelligencer 1