Topologie und Datenanalyse

Seminar Topologie, SoSe2010

Überblick

Wissenschaftler aller Couleur sammeln heutzutags enorme Datenmengen. Der Flaschenhals wird mehr und mehr deren Auswertung. Insbesondere sollen die entscheidenden qualitativen Informationen effizient ermittelt werden (oft aus verrauschten, hochdimensionalen Daten, die in unnatürlichen Koordinaten vorliegen). Topologie ist (vom Standpunkt der Geometrie in der reinen Mathematik) die Teildisziplin, welche genau diese Aufgabe leistet. Im letzten Jahrzehnt gibt es sehr aktive Entwicklungen dies auch in der Praxis umzusetzen.

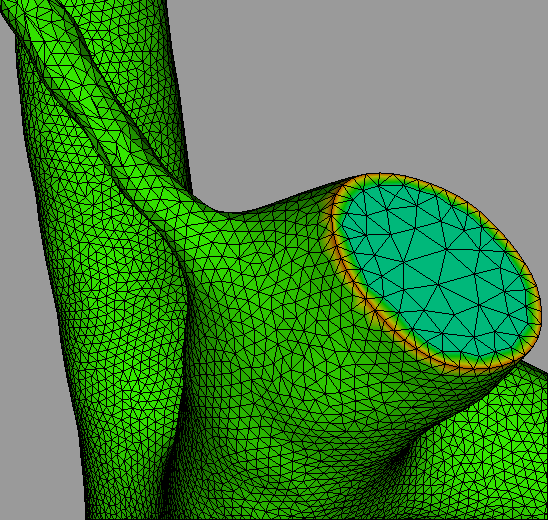
Beispielhafte Frage: in einem Scan von Zellmembranen sollen die verschiedenen Komponenten voneinander unterschieden, Verbindungen entdeckt werden (insbesondere zeitliche Veränderungen), aber dies bei verrauschten Daten: irrelevante Artefakte müssen unterdrückt werden. Erst einmal müssen die Daten in geeigneter geometrischer Weise dargestellt werden.

Simpliziale Komplexe sind ein Beispiel einer solchen Darstellung. Sie bestehen aus einer Vereinigung von Simplizes verschiedener Dimension, die nach bestimmten Regeln zusammengeklebt werden. Diese "Regeln" werden rein kombinatorisch kodiert.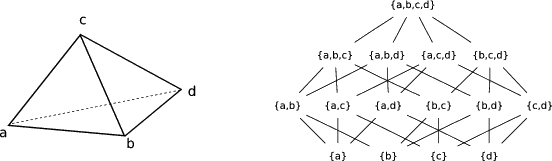

Weiter untersucht man das umgekehrte Problem der Realisierung : wie bekommt man aus rein kombinatorischer Information über ein geometrisches Objekt (wie zum Beispiel einer endlichen Menge von Punkten auf eine Fläche) eine sinnvolle Darstellung dieses Objektes und seiner Geometrie? Wie zählt man die Komponenten, die Löcher?

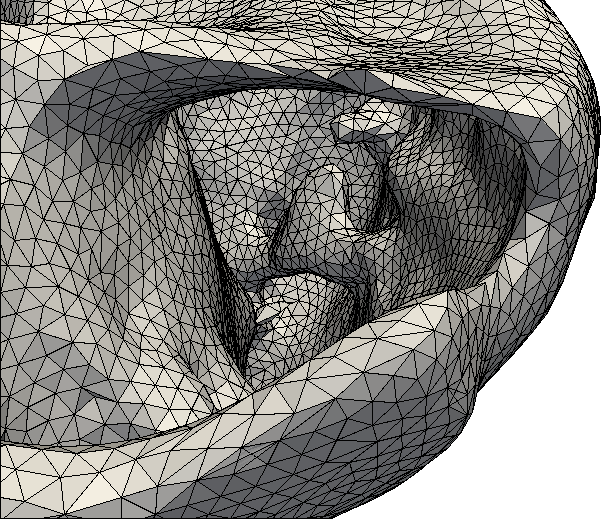
Ganz konkret stellen sich Fragen wie: aus einer Menge von Punkten in Raum, welche (Zentren von) Atomen eines gro&szuml;en Moleküls festlegen, effizient Kavitäten oder Tunnel im Molekül bestimmen, oder Rekonstruktion von (Ober)flächen aus Datenpunkten.

Programm

Dieses Seminar wird am Mathematisches Institut angeboten, aber wir möchten auch sehr gerne interessierte Studenten aus der angewandten Mathematik aufnehmen. Wir werden keine Vorkenntnisse aus der Topologie voraussetzen, sondern diese erarbeiten. Sobald wir das Profil und die Interessen der Teilnehmer kennen, werden wir ein genaueres Programm ausarbeiten. Zu den Themen gehören: Die wichtigsten topologischen Grundlagen: Spezielle Entwicklungen der ``Topologie der Datenanalyse'' sind insbesondere Anwendungen werden gegeben Konkretes Vortragsprogramm:
Nr Thema Quelle Name Termin
1 Simplizialkomplexe EH, (Z) Nikolai Deuschle 06.04.2010
2 Homologie: Einführung EH, (Z) Jan Hendrik Hofmann 13.04.2010
3 Homologie II EH, (Z) Johannes Neumann und Benjamin Heuer 20.04.2010
4 Cech- und Ripskomplexe EH III.2 Johannes Spille und Robert Hesse 27.04.2010
5 sphärische Inversion, Voronoi-Zerlegung EH III.3, E Johannes Steiner 04.05.2010
6 Delaunay- und alpha-Komplexe EH III.3, III.4, E Martin Holzke 11.05.2010
7 Persistente Homologie EH VII.1, Z, 6.1 Simon Naarmann 18.05.2010
8 Algorithmen für (persistente) Homologie EH IV.2, VII.1, Z Kap 7 (?) Matthias Garbs 25.05.2010
9 Algorithmus: Homologie von Teilmengen in R3 EH V.4, DE Simon Beier 01.06.2010
10 Stabilität von persistenter Homologie EH VIII.2 David Ellenberger 08.06.2010
11 Kombinatorische Morse-Theorie für Entrauschen BLW 2-3 Malte Dehling 15.06.2010
12 Optimaler Entrauschungsalgorithmus für Funktionen auf Flächen BLW 4--5 Carolin Homann und Yassin Sabih 22.06.2010
13 Anwendung: 1-dimensionale Gen-Expression EH IX.1 Michael Mathe 29.06.2010
14 Anwendung: Taschen in Proteinen EH IX.2, GJ1 Corinna Krüger 06.07.2010
  1. Simplizialkomplexe (EH III.1, Mu 1.1, 1.2 auch Z 2.3):
    Grundidee: kombinatorische Beschreibung geometrischer Objekte.
    Inhalt: geometrische, abstrakte Simplizialkomplexe, geometrische Realisierung, Triangulierung, Unterteilung, simpliziale Approximation.

  2. (Simpliziale) Homologie (EH IV.1, IV.2-Anfang, Mu 1 (Auswahl), Z 4.2, EH III.2):
    Grundidee: berechenbare Invarianten, welche grundlegende Eigenschaften eines geometrischen Objekts kodieren.
    Inhalt: Zyklen, Ränder, Homologie, Beispielrechnungen, Euler Charakteristik, knapp: Z-und andere Koeffizienten; Homotopie, Homotopieäquivalenz (Teil von EH III.2)

  3. Homologie II (EH IV.3, IV.4, Mu 1,2 (Auswahl)):
    Grundidee: wichtige fortgeschrittene Eigenschaften von Homologie, auch Berechnungsmethoden. relative Homologie, Paarsequenz, exakte Sequenzen, Mayer-Vietoris, Beispielrechnungen

  4. Cech- und Rips-Komplex (EH III.2):
    Grundidee: Vereinfachung eines geometrischen Objekts, indem geeignete Überdeckungen und die Kombinatorik des Schnittverhaltens der Überdeckungsmengen betrachtet wird.
    Inhalt: Überdeckungen, Nerv, Nerv-Theorem, Cech-Komplex und Rips-Komplex

  5. sphärische Inversion, Voronoi-Zerlegung (EH III.3, E):
    Grundidee: klassische geometrische Konstruktionen, um einer diskreten Punktmenge eine sinnvolle "Aufdickung'' zuzuordnen.
    Inhalt: sphärische Inversion, stereographische Projektion, Voronoi-Zellen, Voronoi-Zerlegung, Lift zur höheren Dimension; Gewichte eventuell kurz erwähnen, oder weglassen.

  6. Delaunay- und -Komplexe (EH III.3,III.4, E):
    Grundidee: verfeinerte kombinatorische Beschreibung von aufgedickten diskreten Teilmengen.
    Inhalt: Delaunay-Komplex, Delaunay-Triangulierung, -Komplex, Filtrierung durch Hasse Diagramm, kritische Übergänge und regulärer Kollaps.

  7. Persistene Homologie (EH VII.1, Z 6.1 (Teil)):
    Grundidee: geschickte Nutzung von Topologie/Homologie, um relevante Informationen über geometrische Objekte halbautomatisch zu erhalten.
    Inhalt: Zusammenhangskomponenten-Beispiel, Vorrang des Älteren, Persistene Homologie, Persistenz-Diagramme, Beispiele (siehe insbesondere auch Z)

  8. Algorithmen für persistente Homologie (EH IV.2, VII.1, Z 7.3):
    Grundidee: praktisch verwendbare Algorithmen zur Berechnung persistenter Homologie.
    Inhalt: Matrix Reduktion für Homologie und persistente Homologie -- Beschreibung von Algorithmen, Beispiele und Analyse; (eventuell: sparse matrix technique).

  9. Algorithmus: Homologie von Unterkomplexen von (EH V.4, DE):
    Grundidee: für die spezielle (aber praktisch relevante) Situation einer Teilmenge des effizienten Algorithmus zur Homologieberechnung.
    Inhalt: Schwerpunkt ist der Algorithmus; ggf. knappe Behandlung von Alexander-Dualität.; mögliche Erweiterung: Nutzung für effiziente Algorithmen zu Persistenz (EH VII.2)

  10. Stabilität von Persistenz (EH VIII.2):
    Grundidee: Persistene Homologie ändert sich wenig, wenn die Daten sich wenig ändern.
    Inhalt: Flaschenhals-Metrik, Flaschenhals-Stabilität (für zahme Funktionen), Wasserstein-Metrik, Wasserstein-Stabilität (weniger Details). Mögliche Erweiterung: Berechungsaspekte (EH VIII.1)

  11. Kombinatorische Morse-Theorie für Entrauschen (BLW 2-3, F1, F2, AGHLM):
    Grundidee: kombinatorischer Prozess, um Funktionen auf einem Simplizialkomplex zu entrauschen/vereinfachen.
    Inhalt: kombinatorische Morsefunktionen, kombinatorische Vektorfelder, Auslöschung kritischer Zellen, Dualität für Flächen

  12. Optimaler Entrauschungsalgorithmus für Funktionen auf Flächen (BLW 4-5):
    Grundidee: effizienter Algorithmus, welcher auf einer Fläche eine Funktion optimal entrauscht.
    Inhalt: Beschreibung des Algorithmus, Diskussion.

  13. Anwendung: 1-dimensionale Gen-Expression (EH IX.1):
    Grundidee: bei Entwicklung des Wirbeltier-Embryos steuern periodisch aktive Gene die Entwicklung der Wirbelsäule (mit verschiedener Anzahl von Wirbeln); aber welche? -- Analyse mit persistenter Homologie

  14. Anwendung: Taschen in Proteinen (EH IX.2, GJ1):
    Inhalt: Beschreibung des Problems, Diskussion des 1-dimensionalen ``Spielzeug-Falls'' aus EH; kurze Diskussion des Ansatzes aus (GJ1)

Literatur

  1. (AGHZM) Attali, Glisse, Hornus,Lazarus, Morozov: Persistence-sensitive simpli cation of functions on surfaces in linear time
  2. (BLW) Bauer, Lange, Wardetzky: Optimal topological simplification of discrete functions on surfaces.
  3. (C) Carlsson, Gunnar: Topology and Data (Übersichtsartikel)
  4. (DE) Delfinado and Edelsbrunner, H.: An efficient algorithm for Betti Numbers of Simplicial Complexes
  5. (E) Edelsbrunner, H.: The union of balls and its dual shape, Discrete Comp. Geom. 13, 415-440 (1995)
  6. (EH) H. Edelsbrunner and J. Harer, Computational Topology. An Introduction, Amer. Math. Soc., Providence, Rhode Island, 2009.
  7. (EMP) Edelsbrunner, Moroov, Pascucci: Persistence-sensitive simplification functions on 2-manifolds
  8. (F1) R. Forman: Morse theory for cell complexes. Advances in Mathematics, 134(1):90-145, 1998.
  9. (F2) R. Forman. A user's guide to discrete Morse theory. Seminaire Lotharingien de Combinatoire, B48c: 1-35, 2002.
  10. (GJ1) Giesen and John: The flow complex: a data structure for geometric modelling
  11. (GJ2) Giesen and John: Computing the weighted flow complex
  12. (KMM) T. Kaczynski, K. Mischaikow and M. Mrozek, Computational homology, Applied Mathematical Sciences, vol. 157, Springer, 2004.
  13. (Mi) J. Milnor, Morse theory, Annals of Mathematics Studies, No. 51, Princeton University Press, 1963.
  14. (Mu) J. R. Munkres, Elements of algebraic topology, Addison-Wesley Publishing Company 1984.
  15. (RS) C. Rourke and P. J. Sanderson, Introduction to piecewise-linear topology, Springer, 1982.
  16. (Z) A. J. Zomorodian, Topology for computing, Cambridge Monographs on Applied and Computational Mathematics, vol. 16, Cambridge University Press, 2005.

    17. Scheinerwerb

    Notwendig für den Erwerb der Kreditpunkte sind: The heart images above are courtesy of Olivier Rousseau